343***. Integer Break

Leetcode343 Integer Break

题目

Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.

For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).

**

Note*: You may assume that n* is not less than 2 and not larger than 58.

Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.

大意

给定一个正数n,可以将其分割成多个数字的和，若要让这些数字的乘积最大，求分割的方法（至少要分成两个数）。算法返回这个最大的乘积。

解法1 记忆化搜索

class Solution {
public:
    int vec[60]={0};
    int Break(int n)
    {
        if(n==1) return 1;
        if(vec[n]!=0) return vec[n];
        int res=-1;
        for(int i=1;i<n;i++)
        {
            res =max(max(res,i*Break(n-i)),i*(n-i));
            // i*(n-i)是不对后面(n-i)进行分割，i*Break(n-i)是对后面(n-i)进行再分割。
        }
        vec[n]=res;
        return res;
    }
    int integerBreak(int n) {   
        return Break(n);
    }
};

思路1

使用记忆化搜索的方法，也就是暴力回溯加数组的方法，首先要求n的乘积最大，则

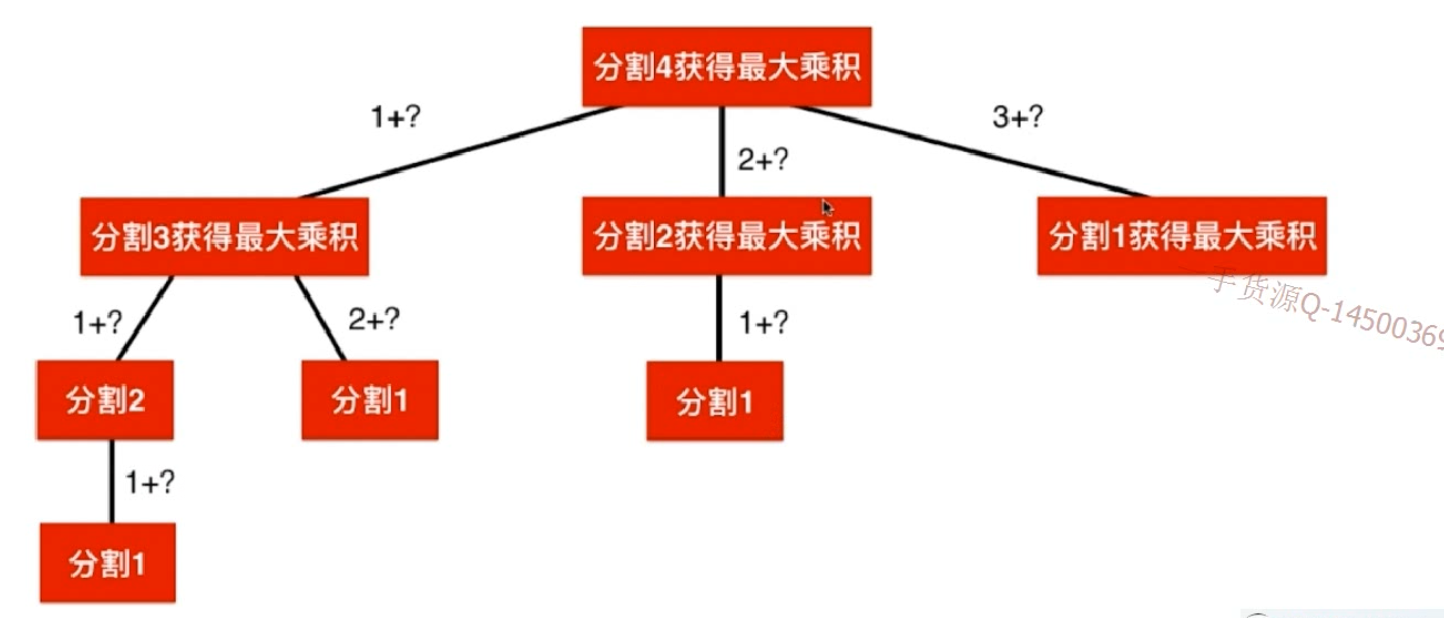
不断的从1开始分割。

• 动态规划法

class Solution {
public:
    int vec[60]={0};
    int Break(int n)
    {	//vec[i]代表表示将数字i分割(至少两份)后得到的最大乘积。
        vec[1]=1;
        for(int i=2;i<=n;i++)
        {
            for(int j=1;j<i;j++)
            {
                vec[i]= max(max(vec[i],j*(i-j)),j*vec[i-j]);   
            }
        }
        return vec[n];
    }
    int integerBreak(int n) {   
        return Break(n);
    }
};

思路2

上面用一个二重循环的动态规划进行求解。

首先memo[1]表示1的最大乘积。

那么memo[2] 就等于max3(memo[2],1*1,1*memo[1])

首先第一层的循环是通过memo[1]得到memo[2]，通过memo[2]得到memo[3] ,通过memo[3]得到memo[4]等等。

里面的第二层循环是为了求把memo[i]分成1,i-1,2,i-2,3,i-3等等，然后找出他们的最大值。