递归的时间复杂度分析

这种情况下，当没有找到target时，或者在左半部分递归继续寻找，或者在右半部分继续寻找，也就是在一次递归中，最多再进行一次递归调用，这时，时间复杂度就是递归的最大深度。（同时，处理时是O(1)的）

总结：如果在递归函数中，只进行一次递归调用，递归深度为depth,在每个递归函数中，时间复杂度为T,则总体时间复杂度为O(T*depth)。

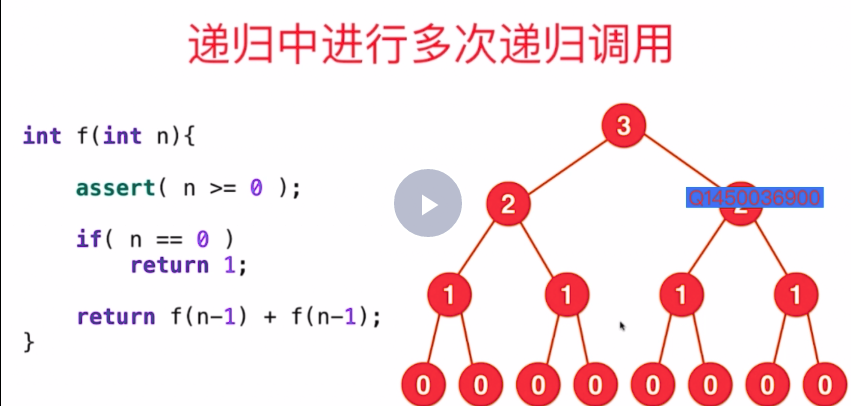
此时主要需要关注调用的次数，可以画一颗递归树，像上图一样的，节点的个数就是调用的次数。

所以这个函数是2^0+2^1+2^2+2^3+2^4+...+2^n=O(2^n)

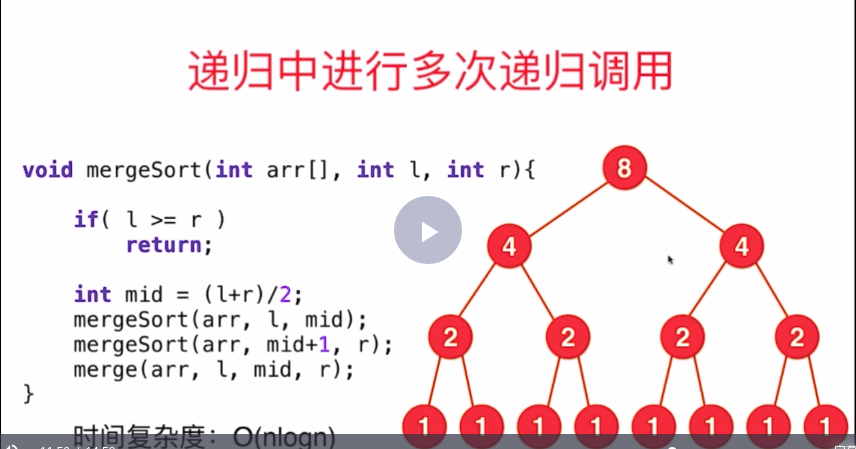
在归并排序中，每次处理的元素规模是逐渐变小的，当有8个元素时，树只有三层。每一层处理的规模都是8（8，4+4，2+2+2+2）所以总体是O(nlogn)

Contents