79. Word Search

题目

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

a) Insert a character
b) Delete a character
c) Replace a character

大意

给定两个单词,求两个变成相同的最少步骤.

答案

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1 = word1.size();
        int len2 = word2.size();
        int dp[len1+1][len2+1];
        for(int i=0;i<=len1;i++)
        {
            dp[i][0] =i;
        }
        for(int i=0;i<=len2;i++)
        {
            dp[0][i]=i;
        }
        for(int i=1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(word1[i-1]==word2[j-1]) dp[i][j] = dp[i-1][j-1];// 十分容易搞错下标
                else
                {
                    dp[i][j] =min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;
                }
            }
        }
        int a = dp[len1][len2];
        return a;
    }
};

思路

如果要计算单词”INTENTION”和单词”EXECUTION”之间的编辑距离，那么该怎么计算呢？

首先，把这个问题简单化。把上面两个单词简化为长度为1的两个单词I和E。

如果要“I”变化为”E”，可以把”I”替换为”E”
如果要“I”变化为空串” “，可以把”I”删除，从而形成””
如果要空串“ ”变化为”E”，可以把”E”插入，从而形成E

上面三种变化分别表示替换，删除，插入这三种基本操作。

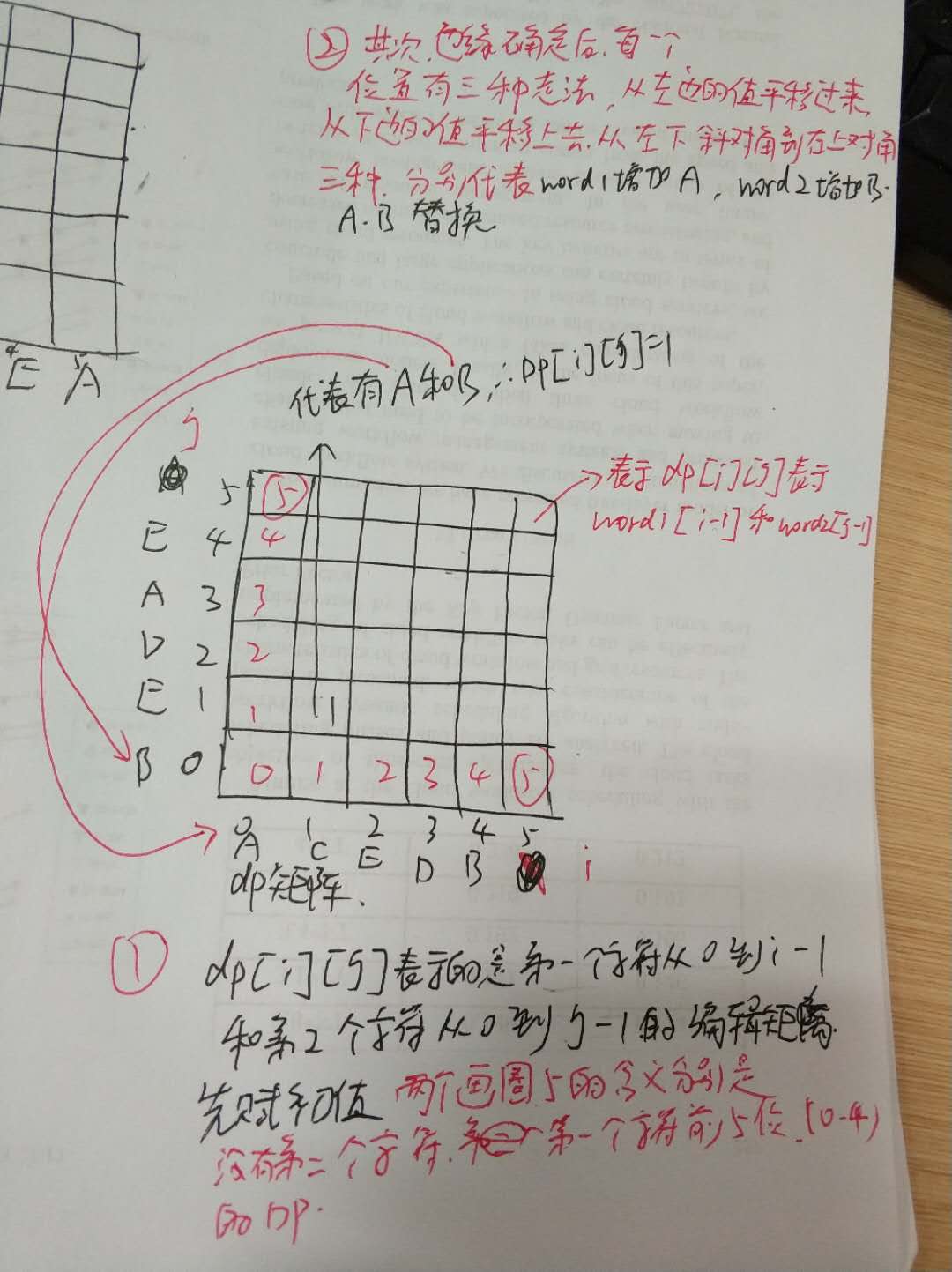
接下来，定义一个表达式D(i,j)。它表示从第1个字单词的第0位至第i位形成的子串和第2个单词的第0位至第j位形成的子串的编辑距离。

显然，可以计算出动态规划的初始表达式，如下:

D(i,0) = i

D(0,j) = j

然后，考虑动态规划的状态转移方程式，如下:

​ D(i-1, j) + 1
D(i,j)=min ( D(i, j-1) + 1 )
​ D(i-1, j-1) +2( if X(i) != Y(j) ) ; D(i-1,j-1) ( if X(i) == Y(j) )

上面的状态转移方程的含义是，D(i,j)的值，要么是D(i-1, j)的操作完成之后删除一个字符(第1个单词的第i个字符)，要么是D(i, j-1)的操作完成之后增加一个字符(第2个单词的第j个字符)，要么是D(i-1, j-1)的操作完成自后替换一个字符(如果第1个单词的第i个字符和第2个单词的第j个字符不等)(意思是已经知道dp[i-1][j],现在求dp[i][j]要么把多出来的i 删除,要么补一个j)，或者是D(i-1, j-1)的操作完成自后什么也不做(如果第1个单词的第i个字符和第2个单词的第j个字符相等)。

接着便是定义了,这里定义dp[i][j] 为第一个单词 从0到i-1 和第二个单词从0到j-1 的编辑距离.